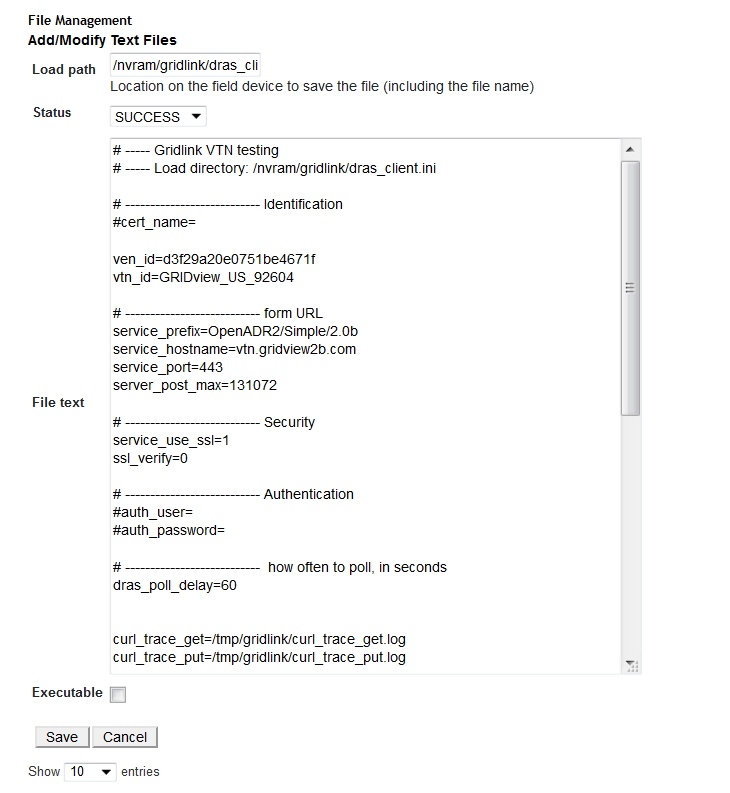
INI Configuration Parameters 2.0b

GRIDview

Load a Pre-configured text file to connect to VTN

Device / Files  /nvram/gridlink/dras_client.ini

Identification

   ven_id     Vitual End Node Identification Name

   vtn_id     Virtual Top Node Identification Name

URL

   service_prefix      Path  of the VTN URL

   service_hostname     Hostname of VTN URL (Should end with .com)

SECURITY ==

service_use_ssl     Enable SSL when communicating with the server. (1=enable, 0 = disable, enabled by default)

ssl_verify     Enable SSL certificate verification when communicating with the server. Disable when trouble shooting connection problems. When SSL verification fails, temporarily disabling ssl_verify can re-establish communication. (1=enable, 0 = disable, enabled by default)

HTTP (password) authentication

     auth_user     Username     (must be blank for X.509 Certificate Authentication)

     auth_password     Password     (must be blank for X.509 Certificate Authentication)

OPTIONS ==

log_level     Set logging verbosity. Each higher level includes all the lower levels. Configurable values are:

DEBUG1, DEBUG2, DEBUG3, DEBUG4, DEBUG5
INFO
NOTICE (Default)
WARNING
ERROR
LOG
FATAL
PANIC

eievent_enabled     Enable eiEvent service. (1=enable, 0 = disable, enabled by default)

eiopt_enabled     Enable eiOpt service. (1=enable, 0 = disable, enabled by default)

eiregisterparty_enabled     Enable eiRegisterParty service. (1=enable, 0 = disable, enabled by default)

eiregisterparty_use_cached     Use previous registration details when starting up.(1=enable, 0 = disable, enabled by default)

eireport_enabled     Enable eiReport service. (1=enable, 0 = disable, enabled by default)

OPT-OUT/OPT-IN ==

Configurable through I/O registers or INI parameters, the opt-out service implementation on GridLink assumes opt-in unless otherwise specified.

When I/O register values are specified, they override INI parameter values.

A duration of 0 specifies an open-ended opt-out period. Both parameters must be present in the INI file to be valid. Opt start times in the
distant past may be ignored.

opt_type  – 0 to opt-out, 1 to opt-in.

opt1_start  –  Time (unix epoch, seconds since 1970-01-01 00:00 UTC) to start first opt-out period.

opt1_duration  –  Duration in seconds for first opt-out period.

opt2_start  –  Time (unix epoch, seconds since 1970-01-01 00:00 UTC) to start second opt-out period.

opt2_duration – Duration in seconds for second opt-out period.

ADVANCED ==

curl_trace_get  –  File to store results of HTTP requests.

dras_poll_delay  –  Time in seconds between polls for events.

dras_poll_jitter  –  Randomization time for server polls.

max_disconnect_delay  –  Time the GridLink will allow communication to the VTN to be offline before deleting current event information and returning to normal mode (seconds).

max_execdisconnect_delay  –  Time during an active event the GridLink will allow communication to the VTN to be offline before deleting current event information and returning to normal mode (seconds).

report_poll_delay  –  Time in milliseconds between calls to the report logic. This should be less than the minimum report item sample time.

report_send_delay  – (proposed) Time in seconds between attempts to post report data on the server. Actual post interval is determined by the server oadrCreatedReport and the defined server_post_max.

report_type – Integer specifying the report type 0=usage, 1=delta. Other report types may be defined in the future per the OADR specification.

revision  –  Optional long integer indicating the configuration version. This is output to LO:1 for monitoring by other software.

REPORTS ==

We support telemetry usage reports and telemetry delta usage reports. The items specified for reporting in the configuration will
be offered to the VTN if the VTN registers the report.

Both report types may have one or many variables. Each variable has its own sampling characteristics. GridLink proposes the report
contents and send frequency, but ultimately sends reports as specified by the VTN. The only exception to this is where server_post_max forces more frequent posts to the VTN.

Suppose a report item has a minimum sample period of 4 seconds and a maximum sample period of 1 minute. If the value does not change, the item will be sent every 60 seconds regardless of other recorded items. The value is sampled once every 4 seconds and will be sent immediately if it changes.

The main report configuration file is called usage_report.config, in CSV format. A sample file with a few examples is provided with each
GridLink.

Each configuration line contains the following items, separated by commas.

id  –  Unique integer ID of the measurement
name  –  Description of the measurement
item_type  –  One of voltage, energyApparent, energyReactive, energyReal, powerApparent, powerReactive, powerReal. See Item Types, below.
reading_type  –  One of Direct Read, Net, Allocated, Estimated, Summed, Derived, Mean, Peak, Hybrid, Contract, Projected, x-RMS,
x-notApplicable. See Reading Types, below.
iotype  –  I/O type to read. See I/O Types, below.

register  –  Register number to read.
raw_min
raw_max
eng_min
eng_max  –  Scaling parameters for the specified register value.
scalecode  –  Magnitude of the measurement. See Scale Codes, below.
min_period
max_period
onchange  –  Set to 0 or 1.  If 0, record every min_period.  If 1, scan at min_period, record on change, record at least every max_period.
hz  –  integer indicating AC frequency, usually 50 or 60 (optional)
voltage  –  integer, such as 120, 240, 480 (optional)
ac  –  1 or 0, indicates values are in AC (optional)

I/O Types ==
0 Analog Input (signed 16 bits)
1 Analog Output (signed 16 bits)
10 Discrete Input
11 Discrete Output
20 Long Input (signed 32 bits)
21 Long Output (signed 32 bits)
22 Float Input (32 bits)
23 Float Output (32 bits)

== Item Types (from oadr_power_20b.xsd) ==
voltage Voltage
energyApparent Apparent Energy, measured in volt-ampere hours (VAh)
energyReactive Reactive Energy, volt-amperes reactive hours (VARh)
energyReal Real Energy, Watt Hours (Wh)
powerApparent Apparent Power measured in volt-amperes (VA)
powerReactive Reactive power, measured in volt-amperes reactive (VAR)
powerReal Real power measured in Watts (W) or Joules/second (J/s)

Reading Types (from oadr_ei_20b.xsd) ==

Direct Read Reading is read from a device that increases monotonically, and usage must be computed from pairs of start and stop
readings.
Net Meter or [resource] prepares its own calculation of total use over time.
Allocated Meter covers several [resources] and usage is inferred through some sort of pro data computation.
Estimated Used when a reading is absent in a series in which most readings are present. Summed Several meters together provide the reading for this [resource]. This is specifically a different than aggregated, which refers to multiple [resources] in the same payload.
See also Hybrid.
Derived Usage is inferred through knowledge of run-time, normal operation, etc.
Mean Reading is the mean value over the period indicated in Granularity
Peak Reading is Peak (highest) value over the period indicated in granularity. For some measurements, it may make more sense as the lowest value. May not be consistent with aggregate readings. Only valid for flow-rate Item Bases, i.e., Power not Energy.
Hybrid If aggregated, refers to different reading types in the aggregate number.
Contract Indicates reading is pro forma, i.e., is reported at agreed upon rates
Projected Indicates reading is in the future, and has not yet been measured.
x-RMS Root Mean Square
x-notApplicable Not Applicable

Scale Codes ==
p Pico 10^-12
n Nano 10^-9
micro Micro 10^-6
m Milli 10^-3
c Centi 10^-2
d Deci 10^-1
k Kilo 10^3
M Mega 10^6
G Giga 10^9
T Tera 10^12
none Native Scale